Урок 11. Досліджуємо ділення з остачею
Вступ
Ти вже знаєш чотири арифметичні дії: додавання, віднімання, множення і ділення. Чи завжди можна виконати всі ці арифметичні дії у множині натуральних чисел? Ні, не завжди. Зокрема, якщо неможливо виконати ділення націло, то виконують ділення з остачею. Сьогодні на уроку ти повториш те, що тобі відомо про ділення з остачею, пригадаєш, як його виконувати.
Розминка
Ділення з остачею
1. Називаю всі числа, які менші від діленого й діляться на дільник націло.
2. Найбільше із цих чисел ділю на дільник, результат записую в частці.
3. Віднімаю від діленого знайдене найбільше число, отримую остачу. Записую її в дужках.
Перевірка ділення з остачею
1. Множу неповну частку на дільник.
2. Додаю до одержаного результату остачу.
3. Порівнюю одержаний результат з діленим: якщо одержимо ділене, то ділення з остачею виконане правильно.
Наприклад: 14 : 3
1) 3, 6, 9, 12
2) 12 : 3 = 4 — неповна частка
3) 14 – 12 = 2 — остача, 2 < 3
14 : 3 = 4 (ост. 2)
Перевірка: 4 ∙ 3 + 2 = 14.
Остача має бути меншою, ніж дільник!
a : b = c (ост. r), r < b
Ділення націло можна розглядати як ділення з остачею, яке в остачі дає нуль.
Кількість остач, включаючи нуль, дорівнює дільнику.
Розвязуємо проблемні ситуації
Завдання 1
Різниця двох натуральних чисел a і b існує тоді, коли a більше за b або дорівнює b.
Частка a і b у множині натуральних чисел існує тоді, коли є таке число c, за якого справджується рівність с ∙ b = a.
Завдання 2
Виконуємо вправи
Завдання 3
Завдання 4
Завдання 5
Попрацюй у зошиті
 Визнач вирази, у яких значення неповної частки дорівнює нулю. Виконай ділення з остачею в цих випадках; перевір результати.
Визнач вирази, у яких значення неповної частки дорівнює нулю. Виконай ділення з остачею в цих випадках; перевір результати.
a : b = 0 (ост. a), якщо a < b
41 : 4 35 : 8
74: 9 8 : 27
3 : 9 55 : 8
36 : 8 42 : 5
Завдання 6
Завдання 7
Підсумок
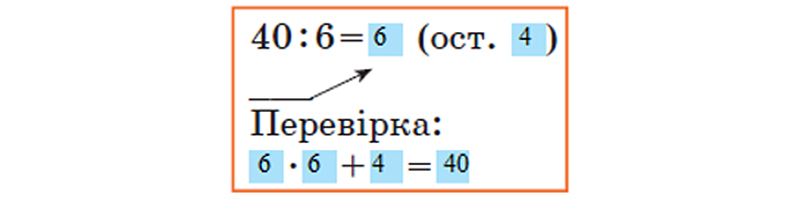 Запиши приклад у зошит та виконай ділення з остачею за зразком.
Запиши приклад у зошит та виконай ділення з остачею за зразком.